
Institute of Applied Analysis
University Ulm
Helmholtzstraße 18
89081 Ulm
Room E.10
Tel.: +49 731 50-23560
andre.schlichting@uni-ulm.de
News and Updates
- Preprint: Formation of clusters and coarsening in weakly interacting diffusions
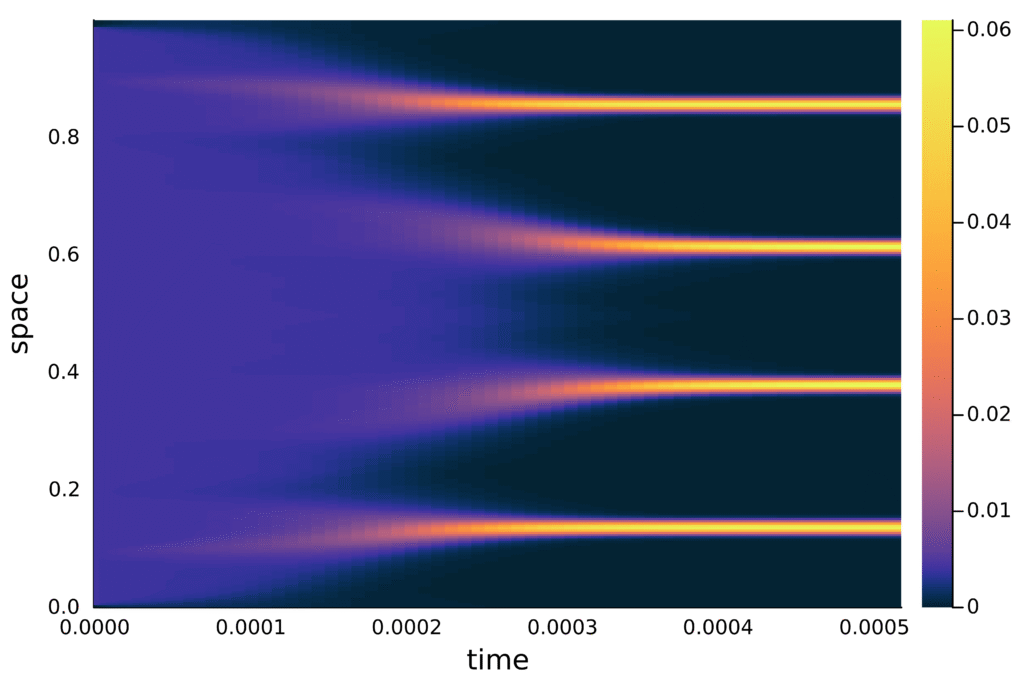
Together with Nicolai Gerber, Rishabh Gvalani, Martin Hairer and Greg Pavliotis, we study the clustering behavior of weakly interacting diffusions under the influence of sufficiently localized attractive interaction potentials on the one-dimensional torus. We describe how this clustering behavior is closely related to the presence of discontinuous phase transitions in the mean-field PDE. For local attractive interactions, we employ a new variant of the strict Riesz rearrangement inequality to prove that all global minimizers of the free energy are either uniform or single-cluster states, in the sense that they are symmetrically decreasing.
We analyze different timescales for the particle system and the mean-field (McKean-Vlasov) PDE, arguing that while the particle system can exhibit coarsening by both coalescence and diffusive mass exchange between clusters, the clusters in the mean-field PDE are unable to move and coarsening occurs via the mass exchange of clusters. By introducing a new model for this mass exchange, we argue that the PDE exhibits dynamical metastability. We conclude by presenting careful numerical experiments that demonstrate the validity of our model. arXiv:2510.17629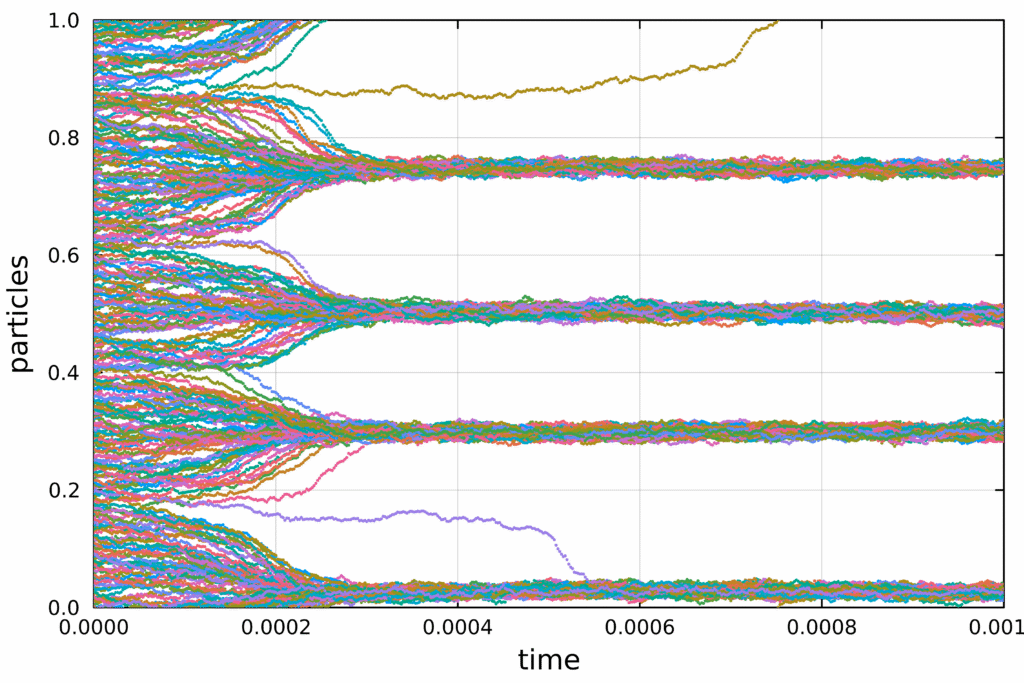
- Preprint: Derivation of the fourth-order DLSS equation with nonlinear mobility via chemical reactions
Together with Alexander Mielke and Artur Stephan, we provide a derivation of the fourth-order DLSS equation based on an interpretation as a chemical reaction network. We consider the rate equation on the discretized circle for a process in which pairs of particles occupying the same site simultaneously jump to the two neighboring sites; the reverse process involves pairs of particles at adjacent sites simultaneously jumping back to the site located between them. Depending on the rates, in the vanishing-mesh-size limit we obtain either the classical DLSS equation or a variant with nonlinear mobility of power type. Via EDP convergence, we identify the limiting gradient structure to be driven by entropy with respect to a generalization of diffusive transport with nonlinear mobility. Interestingly, the DLSS equation with power-type mobility shares qualitative similarities with the fast diffusion and porous medium equation, since we find traveling wave solutions with algebraic tails or compactly supported polynomials, respectively.
For details see arXiv:2510.07149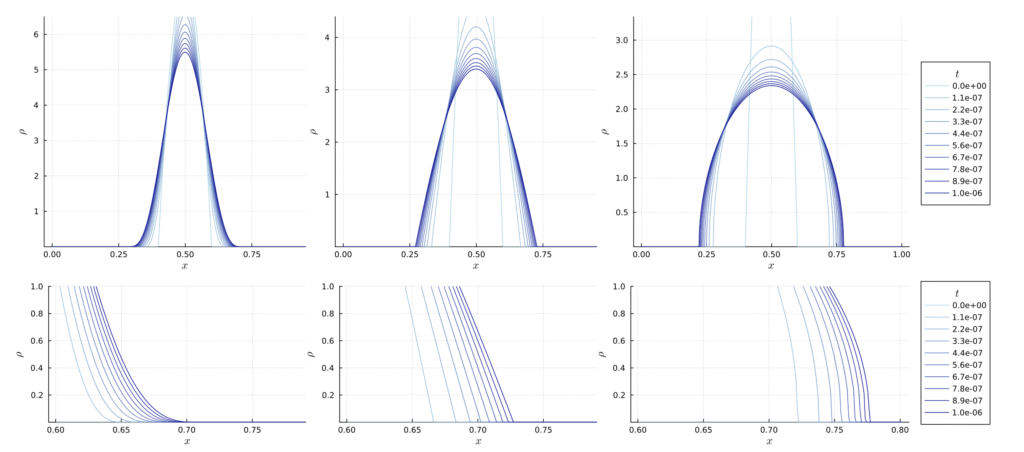
- Preprint: Existence and Non-existence for Continuous Generalized Exchange-Driven Growth model
Together with Chun Yin “Solomon Lam, after the derivation of the continuous generalized exchange-driven growth model in arXiv:2503.21572, we continue the study of the existence and uniqueness of solutions for kernels with superlinear growth at infinity and singularity at the origin. Moreover, we show the non-existence of solutions for kernels with sufficiently rapid growth. The latter result is shown via the finite-time gelation and instantaneous gelation in the sense of moment blow-up. For details see arXiv:2509.05262.
- Extended updated preprint: Variational convergence for an irreversible exchange-driven stochastic particle system
Together with Jasper Hoeksema and Chin Yin Lam, we considerably extended and updated the previous version of the arXiv preprint 2401.06696.
We show the variational convergence of an irreversible Markov jump process describing a finite stochastic particle system to the solution of a countable infinite system of deterministic time-inhomogeneous quadratic differential equations known as the exchange-driven growth model, which has two conserved quantities. As a bounded perturbation of the reversible kernel, the variational formulation is a generalization of the gradient flow formulation of the reversible process and can be interpreted as the large deviation functional of the Markov jump process. As a consequence of the variational convergence result, we show the propagation of chaos of the Markov processes to the limiting equation and the -convergence of the energy functional. The latter convergence is consistent with related results for reversible coagulation-fragmentation equations and reveals the connection of stochastic processes to the long-time condensation phenomena in the limit equation. - Preprint: Convergence of a Stochastic Particle System to the Continuous Generalized Exchange-Driven Growth Model
Together with Chun Yin Lam, we study the continuous generalized exchange-driven growth model (CGEDG) is a system of integro-differential equations describing the evolution of cluster mass under mass exchange. The rate of exchange depends on the masses of the clusters involved and the mass being exchanged. This can be viewed as both a continuous generalization of the exchange-driven growth model and a coagulation-fragmentation equation that generalizes the continuous Smoluchowski equation.
Starting from a Markov jump process that describes a finite stochastic interacting particle system with exchange dynamics, we prove the weak law of large numbers for this process for sublinearly growing kernels in the mean-field limit. We establish the tightness of the stochastic process on a measure-valued Skorokhod space induced by the 1-Wasserstein metric, from which we deduce the existence of solutions to the (CGEDG) system. The solution is shown to have a Lebesgue density under suitable assumptions on the initial data. Moreover, within the class of solutions with density, we establish the uniqueness under slightly more restrictive conditions on the kernel.
arXiv:2503.21572