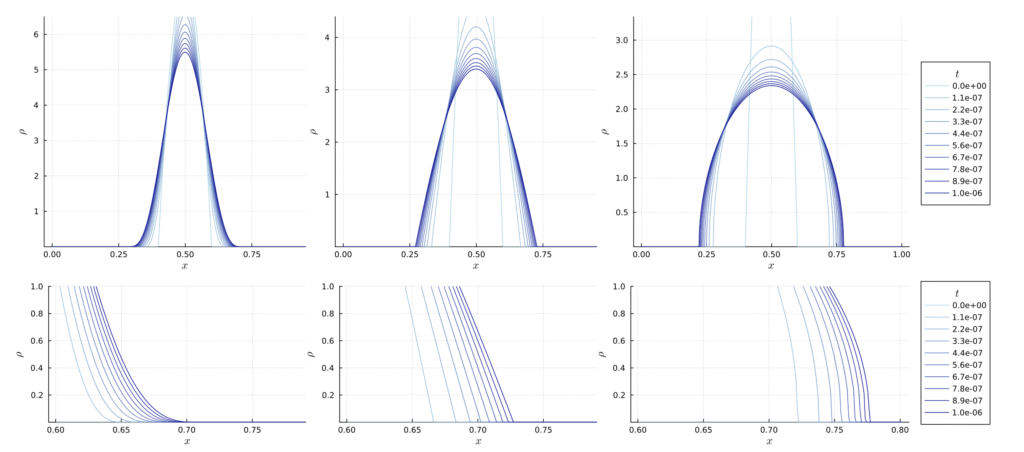
Together with Alexander Mielke and Artur Stephan, we provide a derivation of the fourth-order DLSS equation based on an interpretation as a chemical reaction network. We consider the rate equation on the discretized circle for a process in which pairs of particles occupying the same site simultaneously jump to the two neighboring sites; the reverse process involves pairs of particles at adjacent sites simultaneously jumping back to the site located between them. Depending on the rates, in the vanishing-mesh-size limit we obtain either the classical DLSS equation or a variant with nonlinear mobility of power type. Via EDP convergence, we identify the limiting gradient structure to be driven by entropy with respect to a generalization of diffusive transport with nonlinear mobility. Interestingly, the DLSS equation with power-type mobility shares qualitative similarities with the fast diffusion and porous medium equation, since we find traveling wave solutions with algebraic tails or compactly supported polynomials, respectively.
For details see arXiv:2510.07149