Description
\( \newcommand{\R}{\mathbb{R}} \newcommand{\dx}{\mathrm{d}} \)
The Fokker Planck equation has the form
\[
\partial_t \varrho(x,t) = \nabla \cdot \bigl(\beta^{-1} \nabla \varrho(x,t) + \varrho(x,t) \nabla H(x)\bigr) ,\qquad \varrho(x,0)=\varrho_0(x) ,
\]
where \(H:\R^n\to \R\) is a smooth function, \(\beta>0\) some parameter and \(\varrho_0\) a probability density on \(\R^n\). The partial differential equation is in divergence form and conserves mass. Hence, also \(\varrho(\cdot,t)\) is a probability density on \(\R^n\). In the case, where \(H\) has some growth at \(\infty\), the equilibrium solutions \(\varrho_\infty:\R^n \to \R\) are characterized by
\[ \beta \nabla \varrho_\infty + \varrho_\infty \nabla H =0 \]
leading to the solution
\[ \varrho_\infty(x) = Z^{-1} e^{-\beta H(x)} \quad \text{with} \quad Z = \int e^{-\beta H(x)} \; \dx x \]
The density \(\varrho_\infty\) is called Gibbs distribution, which accounts to the fact, that it minimizes the (Gibbs) free energy
\[ F(\varrho) = E(\varrho) + \beta^{-1} S(\varrho) \]
where \(E\) is the energy and \(S\) the (Gibbs-Boltzmann) entropy
\[ E(\varrho) := \int H \varrho\;\dx x \quad\text{and}\quad S(\varrho) := \int \varrho \log \varrho \; \dx{x} . \]
By this formulation \(\beta\) plays the role of the inverse temperature. Note, that the Euler-Lagrange equation is given by
\[ H(x) + \beta^{-1} \bigl(\varrho(x) + 1\bigr) = 0 , \]
which is solved by \(\varrho_\infty\).
Pathwise formulation via stochastic differential equations
The stochastic process \(X(t)\) defined by
\[ \dx X(t) = – \nabla H(X(t))\;\dx t + \sqrt{2\beta^{-1}} \;\dx W(t) , \quad X(t) = X_0 , \]
where \(W(t)\) is an \(n\)-dimensional Brownian motion, is the pathwise formulation of the Fokker Planck equation. If distribution of the initial random vector \(X_0\) is given by \(\mathrm{law}\; X_0 = \varrho_0\), then at later times the solution \(X(t)\) has distribution \(\mathrm{law}\; X(t) = \varrho(\cdot,t)\), where \(\varrho\) is solution of the Fokker Planck equation.
The dynamic of the pathwise formulation undergoing diffusion in the potential \(H\). The particle is solely described by its position \(X(t)\in \R^n\), i.e. inertia is neglected. Then, the particle chooses the steepest descent with respect ot \(H\), which is perturbed by random fluctuation, which are assumed to be normal distributed. The coupling parameter \(\beta\) describing the strength of the fluctuations plays again the role of inverse temperature. In particular, the limit \(\beta\to \infty\) describes the behaviour of the system without fluctuations.
Ornstein-Uhlenbeck process
A prominent example, which can be explicitly solved, is the Ornstein-Uhlenbeck process, corresponding to the choice
\[ H(x) = \frac{\gamma}{2} | x |^2 . \]
The stationary distribution is given by the Gaussian
\[ \varrho_\infty(x) = \left( \frac{2\pi}{\gamma\beta} \right)^{-\frac{n}{2}} \exp\left(-\frac{\gamma \beta |x|^2}{2}\right) . \]
The underlying picture becomes particular simple in one dimension. There, the leading order behaviour of the process can be characterized by its mean \(m(t)\) and variance \(\sigma(t)\), which are given by
\[ m(t) := \int x \varrho(x,t) \;\dx x \qquad\text{and}\qquad \sigma(t) := \int (x-m(t))^2 \varrho(x,t) \;\dx{x} = \int x^2 \varrho(x,t)\; \dx{x} – m(t)^2 . \]
Both, \(m(t)\) and \(\sigma(t)\), satisfy an ordinary differential equation not depending on \(\varrho\)
\[ \dot m(t) = -\gamma m(t) \qquad \text{and}\qquad \dot sigma(t) = 2\beta^{-1} – 2\gamma \sigma(t) .\]
Hence, the mean converges exponentially fast to \(0\) with rate \(\gamma\) and the variance converges exponentially fast from the initial variance \(\sigma(0)\) to \((\beta \gamma)^{-1}\) with rate \(2 \gamma\)
\[ m(t) = m(0) \; e^{-2\gamma t} \qquad\text{and}\qquad \sigma(t) = \sigma(0) e^{-2\gamma t} + \frac{1}{\beta \gamma} \bigl(1-e^{-2\gamma t}\bigr) . \]
Numerical example
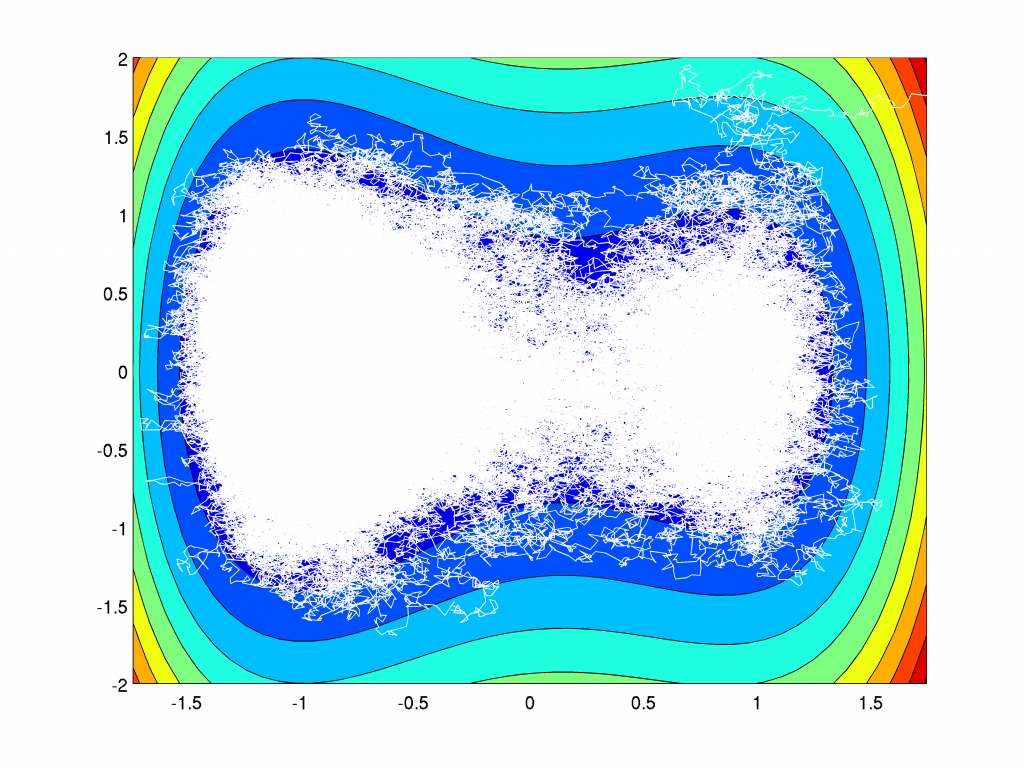
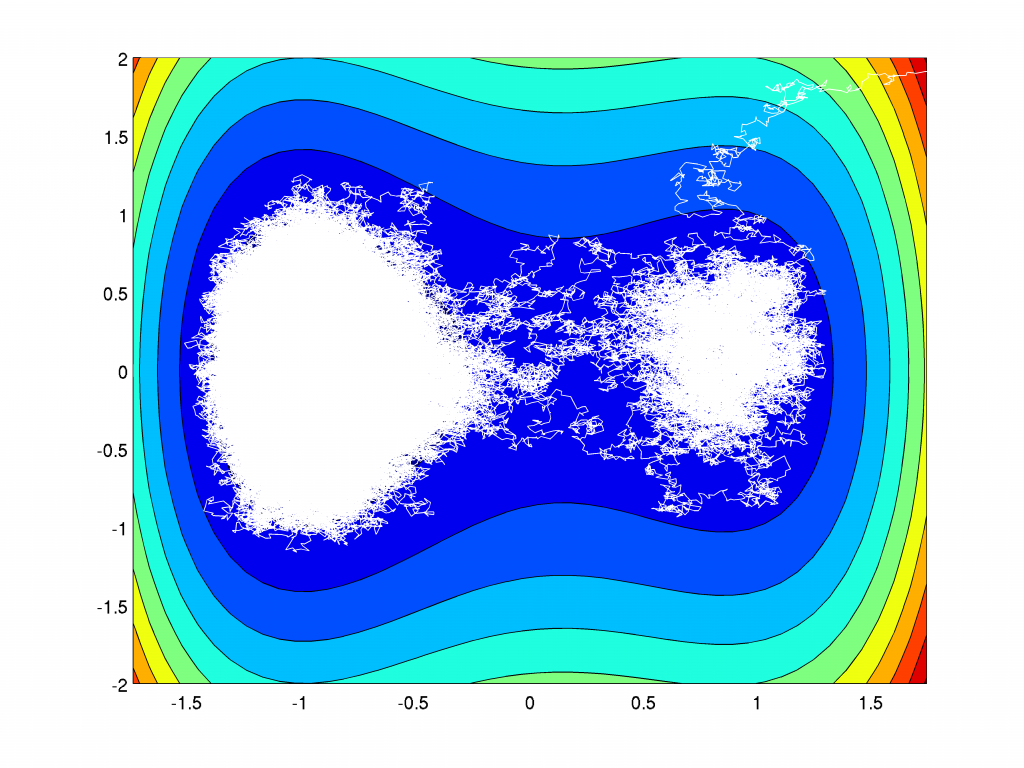
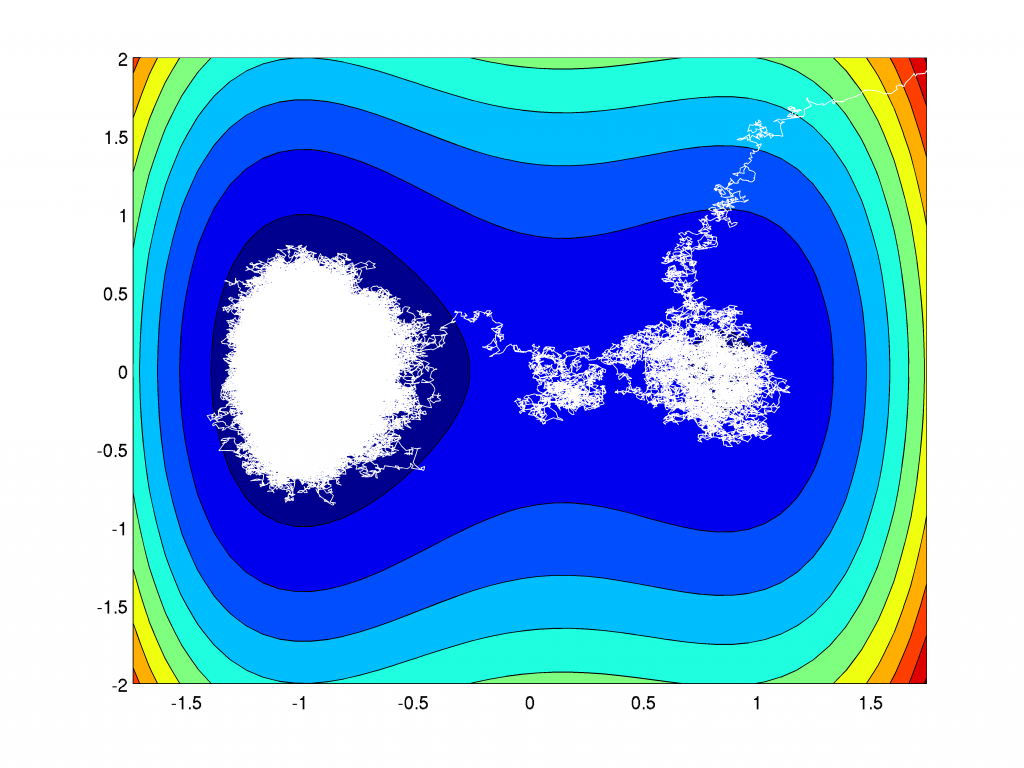
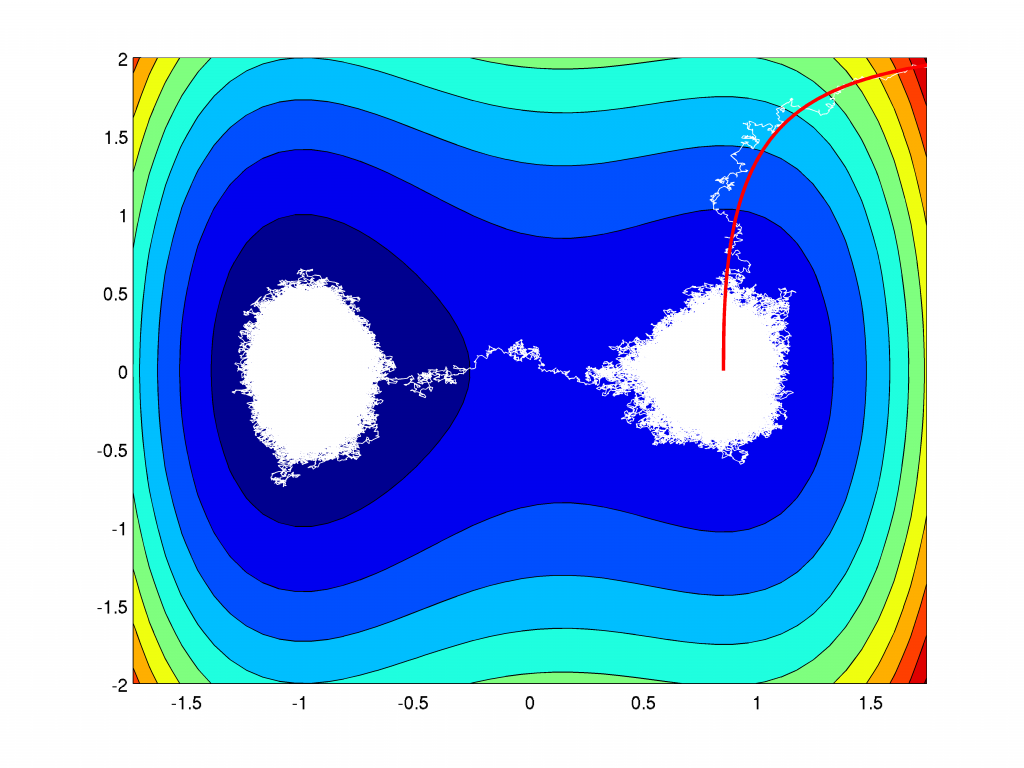
For general potentials \(H\) explicit solutions of the Fokker Planck equation are not available. However, the pathwise formulation allows to do Monte-Carlo simulation of single realisations of the process \(X(t)\). The case, where \(H\) is not convex is especially interessting, because at low temperature, i.e. \(\beta \gg 1\), the process shows metastable behaviour.
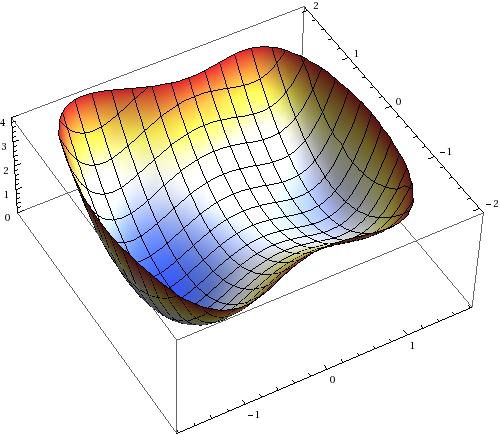
Therefore, we consider the potential function \(H:\R^2 \to \R\) looking like
The realization of the process \(X(t)\) for increasing values of \(\beta\):
For increasing values of \(\beta\) the particle goes quickly to the local minima and is trapped there longer and longer times. The transition to the global energy minimizing state happens along a path crossing the saddle. This behaviour is called metastable. For the limiting dynamic \(\beta=\infty\) without any fluctuation a transition is not possible and the particle is stuck in the local minima.
References
- R. Jordan, D. Kinderlehrer, and F. Otto, “The Variational Formulation of the Fokker-Planck Equation,” SIAM Journal on Mathematical Analysis, vol. 29, no. 1, 1998.
Pingback: Classic results for porous medium equation | André Schlichting
For some reasons the equation are not rendered correctly (Chrome as well as Firefox). What is the actual form of potential used for the numerical simulation? What software did you use to run the simulation? Did you impose Fluctuation Dissipation Relation so that the diffusion coefficeint can be expessed in terms of $\beta$?
Thanks for pointing it out. The equations should be now rendered correctly using MathJax. The potential is a quartic double well like \(H(x,y)= (x^2-1)^2+x + y^2+(x+1)^2/4\). The numerical simulation is a simple explicit Euler discretization of the SDE. I used directly \(\beta^{-1}\) as diffusion coefficient.